Can the number of gear teeth be less than 17?

Gears are a widely used type of component in everyday life, whether it's aviation, cargo ships, automobiles, and so on. However, when designing and processing gears, there are requirements for the number of teeth. Some claim that gears with fewer than 17 teeth cannot rotate, while others point out that there are many gears with fewer than 17 teeth that function properly. Actually, both of these statements are correct. Do you know why?

Why is the number of teeth 17?

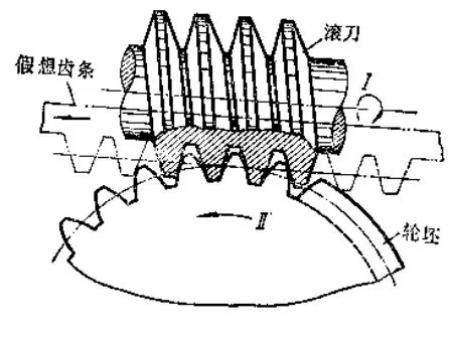
Why is it 17 specifically, and not some other number? As for the number 17, this has to do with the gear manufacturing method. As shown in the figure below, a widely used method is to use a hob to cut.

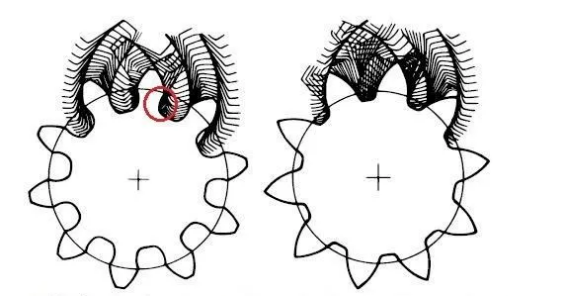
When the number of teeth is small, a phenomenon called undercutting occurs, which affects the strength of the manufactured gear. What is undercutting? It means the root is cut. Pay attention to the red box in the figure:

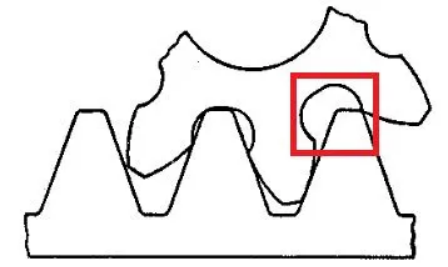
When the intersection of the gear's tooth tip and the pitch line exceeds the limit meshing point of the gear being cut, a portion of the involute tooth profile at the root of the gear is removed. This phenomenon is called undercutting.

So, under what circumstances can undercutting be avoided? The answer lies in the number 17, which corresponds to a tooth tip height coefficient of 1 and a pressure angle of 20 degrees. First, gears can rotate because the upper and lower gears need to form a good transmission relationship. Only when the connection between the two is in place can their operation be a stable relationship. Taking involute gears as an example, good meshing between the two gears can play its role, which is divided into two types: straight-toothed cylindrical gears and helical cylindrical gears. The standard straight gear has a tooth tip height coefficient of 1, a tooth root height coefficient of 1.25, and a pressure angle of 20 degrees When gear processing, if the gear blank and the tool are like two gears. If the number of teeth of the blank is less than a specific value, the root of the tooth will be dug out, which is called undercutting. If the undercutting is too small, it will affect the strength and stability of the gear. The 17 mentioned here is for gears. If we don't talk about the work efficiency of the gear, no matter how many teeth it has, it will work and can operate. In addition, 17 is a prime number, which means the coincidence of a gear tooth and another gear tooth is minimal in a certain number of circles, and the force will not be on the same point for a long time. Gears are precision instruments, although there will be errors on each gear, but the chance of shaft wear caused by 17 is really too large, so if it is 17, it can move for a short time, but it cannot be long-term. However, the issue arises! There are still many gears on the market with fewer than 17 teeth, and they continue to function well, as evidenced by pictures.

However, some netizens have pointed out that, in fact, by changing the manufacturing method, it is possible to produce standard involute gears with fewer than 17 teeth. Of course, such gears are also easy to get stuck (due to gear interference, no picture is found, please imagine), and in this way, it really can't move. There are also many corresponding solutions, offset gears are the most commonly used (vulgarly speaking, it is to move the tool a little bit when cutting), and there are also helical gears, cycloidal gears, etc. There is also a universal cycloidal gear.

Another netizen's viewpoint: It seems that everyone still believes in books too much, and I don't know how many people have thoroughly studied gears in their work. The derivation of the gear teeth being greater than 17 in the mechanical principle course for not producing undercutting is based on the top corner R of the gear cutting tool's front rake face being 0. In fact, how can the tools in industrial production have no R angle? (Without the R angle, the tool is sharp and the stress is concentrated, easy to crack during heat treatment, and easy to wear or crack during use). And even if the tool has no R angle, the maximum number of teeth where undercutting occurs is not necessarily 17 teeth, so the statement that 17 teeth is the condition for undercutting is actually open to discussion! Let's look at a few pictures.

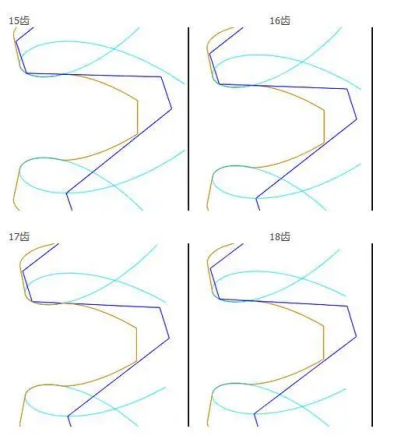
From the figure, it can be seen that when using a tool with the top corner R of the front rake face as 0 to process gears, there is no obvious change in the root transition curve from 15 teeth to 18 teeth. So why is 17 teeth the number of teeth where involute straight teeth start to produce undercutting?

I believe this figure, which illustrates the concept, should be familiar to mechanical engineering students who have used a gear generator. It can be seen that the size of the tool R angle affects the undercutting of the gear.

The purple extended outer epitrochoid curve of the tooth root part in the figure is the tooth profile line after the tooth root is undercut. To what extent will the undercutting of a gear's tooth root affect its use? This is determined by the relative motion of another gear tooth tip and the strength reserve of the gear tooth root. If the tooth tip of the mating gear does not mesh with the undercut part, then these two gears can rotate normally (Note: The undercutting part is a non-involute tooth profile. Meshing a non-involute tooth profile with an involute tooth profile under non-special design conditions is usually non-conjugal, that is, it will interfere).

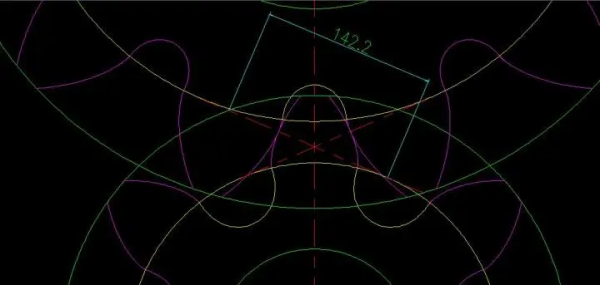
From this figure, it can be seen that the meshing line of these two gears just rubs against the maximum diameter circle corresponding to the transition curve of the two gears (Note: The purple part is the involute tooth profile, the yellow part is the undercutting part, and the meshing line cannot enter below the base circle, because there is no involute line below the base circle. The meshing point of the two gears at any position is on this line), that is, these two gears can just mesh normally. Of course, this is not allowed in engineering, the length of the meshing line is 142.2, and this value / base pitch = overlap ratio.

Some people also say: First, the premise of this question is wrong. The number of teeth less than 17 will not affect the use (the description of this point in the first answer is wrong, the three conditions for correct meshing of gears are unrelated to the number of teeth), but 17 teeth will have some inconveniences in processing under certain specific circumstances. Here is more to supplement some knowledge about gears.

First, let's talk about the involute curve. The involute curve is the most widely used type of gear tooth profile. So why is it an involute curve? What's the difference between this line and a straight line, arc? As shown in the figure below, it is a half-tooth involute curve.

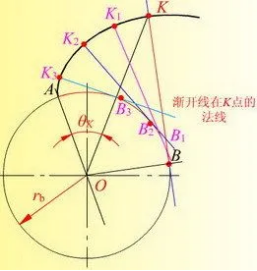
The involute curve can be described in one sentence as the trajectory of an immobile point on a straight line when the line rolls along a circle. Its advantage is obvious. When two involute curves mesh, as shown in the figure below.

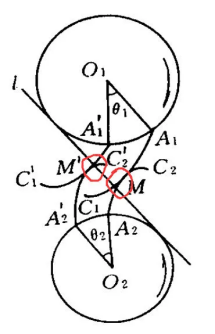
When the two wheels rotate, at the contact point (such as M, M'), the direction of the force is always on the same straight line, and this line is perpendicular to the contact surface (section) of the two involute shapes. Because it is perpendicular, there will be no "slippage" and "friction" between them, which objectively reduces the friction during gear meshing, not only improving efficiency but also extending the life of the gear.

Of course, as the most widely used type of tooth profile - the involute curve, it is not our only choice.

Let's talk about "undercutting" again. As engineers, we not only have to consider whether it is feasible on the theoretical level and whether the effect is good, but more importantly, we have to find ways to present the theoretical things, which involves material selection, manufacturing, precision, testing and other links.

The common processing methods for gears are generally divided into forming method and generation method. The forming method is to directly cut out the tooth shape with a tool that corresponds to the gap shape between the teeth. This generally includes milling cutters, butterfly grinding wheels, etc.; the generation method is more complex, which can be understood as two gears meshing, one gear is very hard (tool), and the other is still in the blank state. The process of meshing is from being far apart gradually moving to the normal meshing state, during which the new gear is cut. If you are interested, you can find "Mechanical Principle" for specific study.

The generation method is widely used, but when the gear has fewer teeth, the tooth top line of the tool and the meshing line will exceed the limit meshing point of the gear being cut, and at this time, the root of the gear being processed will be excessively removed. Since the undercut part exceeds the limit meshing point, it does not affect the normal meshing of the gear, but the disadvantage is that it weakens the strength of the gear. Such gears,when used in heavy-load occasions such as gearboxes, are prone to tooth breakage, as shown in the figure below is the model of a 2-module 8-tooth gear processed normally (with undercutting).

And 17 is the limit number of teeth calculated under the gear standard in our country. Gears with fewer than 17 teeth will have "undercutting phenomenon" when processed normally with the generation method, and at this time, the processing method needs to be adjusted, such as shifting, as shown in the figure below is the 2-module 8-tooth gear processed by shifting (small undercutting).

Of course, the content described here is not comprehensive, and there are many more interesting parts in mechanics. There are also more problems in manufacturing these parts in engineering. Those who are interested in gold powder might as well pay more attention.

Conclusion: The number of teeth 17 comes from the processing method and also depends on the processing method. If you change or improve the gear processing method, such as forming method, shifting processing (here specifically refers to straight-toothed cylindrical gears), there will be no undercutting phenomenon, and there will be no limit to the number of teeth 17.

In addition, from this question and its answers, it can be seen that one characteristic of the mechanical discipline is the high combination of theory and practice.

Netizen's viewpoint: First, the statement that gears with fewer than 17 teeth cannot rotate is incorrect. Let's briefly introduce how the number 17 came about.

Gears are mechanical components with teeth on the rim that continuously mesh to transmit motion and power. Gear tooth profiles include involute, circular arc, etc., and involute gears are more widely used.

Involute gears are divided into straight-toothed cylindrical gears/helical cylindrical gears, etc. For standard straight-toothed cylindrical gears, the tooth tip height coefficient is 1, the tooth root height coefficient is 1.25, and the pressure angle is 20°. Gear processing generally uses the generation method, that is, the movement of the tool and the tooth blank during processing is like a pair of meshing gears. For standard gear processing, if the number of teeth is less than a certain specific value, the involute curve profile at the root of the tooth blank will be cut off, which is called undercutting, as shown in the left figure below. Undercutting will seriously affect the strength of the gear and the smoothness of the transmission. This non-occurring undercutting minimum value is 2*1/sin(20)^2 (1 is the tooth tip height coefficient, 20 is the pressure angle).

The number of teeth 17 here is for standard straight-toothed cylindrical gears. We have many ways to avoid undercutting, such as gear shifting, that is, moving the tool away from or close to the center of the tooth blank rotation. Here, to avoid undercutting, it is necessary to choose to move away from the contour center of rotation, as shown in the right figure below, and the complete involute curve profile comes out again.

After gear shifting, the gear can rotate without being affected. As shown above, by appropriate shifting, a gear with 5 teeth can also rotate. In fact, helical gears can also avoid undercutting or reduce the minimum number of teeth where undercutting occurs.

The number 17 is calculated. It is not that gears with fewer than 17 teeth cannot rotate, but if there are fewer than 17 teeth, it is easy to cut off a part of the involute curve at the root of the gear during gear processing, that is, undercutting, which weakens the strength of the gear. As for how to calculate it, it is entirely a mathematical problem, refer to the formula above, with the meshing angle a=20 degrees, the minimum number of teeth that does not occur undercutting is 17.

Netizen's viewpoint: Whether the number of gear teeth can be less than 17 is a question worth considering. For standard gears, the number of teeth really cannot be less than 17. Why? Because when the number of teeth is less than 17, the gear will have an undercutting phenomenon.

So-called undercutting refers to the condition where the tooth tip line of the tool cuts too much into the root of the gear under certain conditions during gear cutting by the generation method, and a part of the involute curve profile at the root of the gear is cut off.

Generation method

Generation method (also known as the development method) is a gear processing technique that utilizes the envelope principle from geometry. After the involute tooth profiles and the driving gear's angular velocity w1 are given, the driven gear's angular velocity w2 can be obtained through the meshing of the two tooth profiles, and the gear ratio i12 = w1/w2 is a constant value. This is because during the meshing of the two tooth profiles, the two pitch circles perform pure rolling. As pitch circle 1 rolls purely on pitch circle 2, the tooth profile of gear 1 will occupy a series of relative positions with respect to gear 2, and the envelope of these relative positions is the tooth profile of gear 2. In other words, during the pure rolling of the two pitch circles, the two involute tooth profiles can be considered as envelopes of each other.

Undercutting Phenomenon

The cause of undercutting: When the intersection of the tool's tooth tip line and the meshing line exceeds the meshing limit point N1, and the tool continues to move from position Ⅱ, it will cut away a part of the involute tooth profile that has already been machined at the root.

The consequences of undercutting: A gear with severe undercutting, on one hand, weakens the bending strength of the teeth; on the other hand, it reduces the degree of gear transmission, which is very unfavorable for the transmission. The cause of undercutting: When the intersection of the tool's tooth tip line and the meshing line exceeds the meshing limit point N1, and the tool continues to move from position Ⅱ, it will cut away a part of the involute tooth profile that has already been machined at the root.

For non-standard gears, having fewer than 17 teeth is acceptable.

Having said all of this, what is your opinion? Feel free to leave a comment and share~